Más de una vez, hemos escuchado, ¿para qué me sirve? o ¿Dónde se usa? o ¿En qué se aplica?... Preguntas frecuentes que nos hacemos con el uso de las Matemáticas.
A continuación se da el Tema y algunos ejemplos de aplicación:
Tema:
- LOGARITMOS
- para medir la intensidad de un terremoto (en la escala de Richter). Veamos su ecuación

- para describir el decaimiento radiactivo de una sustancia
- para evaluar el comportamiento de una epidemia.
- para calcular cómo crece un determinado capital invertido en un banco a un cierto interés
El químico Sorensen lo definió como el logaritmo negativo de base 10 de la actividad de los iones hidrógeno. Dado por:
Tema:
- FUNCIÓN CUADRÁTICA
Aplicación:
- En la Física: la trayectoria de una pelota lanzada al aire, la trayectoria que describe un río al caer desde lo alto de una montaña, entre otras.

- En ingeniería Civil: en la construcción de puentes colgantes que se encuentran suspendidos en uno de los cables amarrados a sus torres.

- En Biología: estudiar efectos nutricionales de los organismos.
Tema:
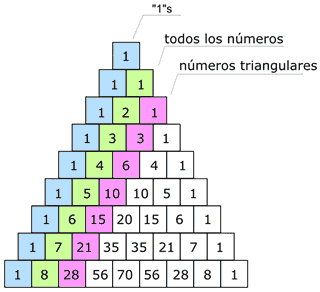
Supongamos que en un torneo de tenis, el entrenador de un equipo X compuesto por 5 grandes tenistas, debe elegir 2 de sus jugadores para un partido de dobles. Es decir hay 5 tenista y el entrenador debe elegir sólo 2. Ahora ¿de cuántas maneras posibles puede formar los dobles este entrenador? Con ayuda de el triángulo obtiene la respuesta.
1º Tiene 5 tenistas. Comenzar a contar las filas desde 0 hasta llegar a la 5º.
2º En esa fila, contar desde 0 hasta 2 (porque son 2 tenistas los grupos que necesitaría). Verá que se posiciona en el primer número 10.
Los 10 posibilidades que tiene este entrenador de elegir sus pares de los 5 tenistas.
![\mbox{pH} = -\log_{10} \left[ \mbox{a}_{H_3O^+} \right]](http://upload.wikimedia.org/math/7/b/7/7b7e772992e9d43888cd421cba60c766.png)